In the past few weeks

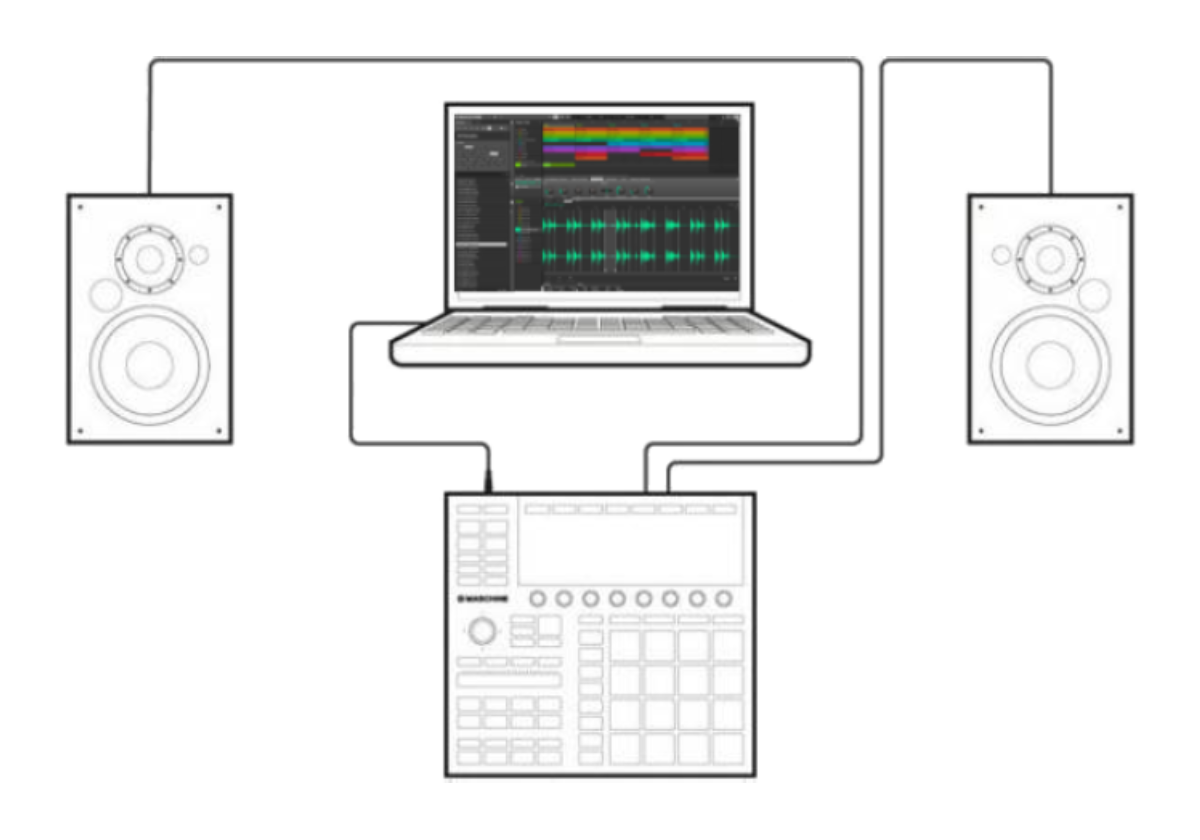
I've been developing a music theory tool for Native Instruments Maschine users, especially for those (like me) who find music theory overwhelming. My goal is to help users understand the harmonic relationship between chords and provide an easy, enjoyable way to create satisfying progressions—even if music theory feels intimidating.

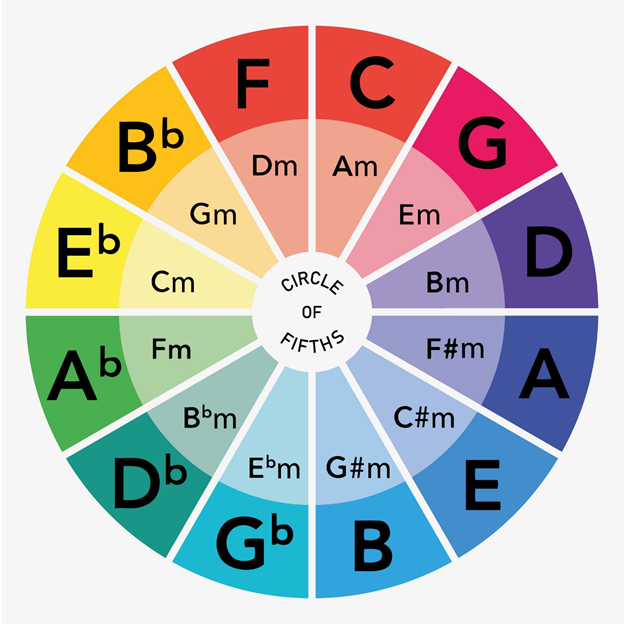
This tool, called "Fif'Chord Finder" represents the beginning of a more advanced project that I plan to expand over time.

Why Create This Tool?

Many Maschine users struggle with using the Circle of Fifths. While Maschine is a powerful tool that provides preset scales and modal chord suggestions, it can still be overwhelming without a foundational understanding of music theory. My tool offers an easy way to explore chord relationships, making creative choices with Maschine's chord mode feel less intimidating and more intuitive.

(Above is a screencap from a thread on modal exchange I generated with NotebookLM. My sources were the previously stated [fixed] chord sets, the Circle of Fifths, and a book on borrowing chords for jazz compositions. This should offer you an example of the kind of progressions users might use my tool to construct and why.)

Key Features So Far

With the help of a coding assisstant, I've made significant progress over the past few weeks:

// Established chord sets
const chordSets = {
    MAJ1: ['C', 'Emi', 'F', 'G', 'Ami', 'Esus4', 'Gadd9', 'Dmi', 'Fadd9', 'F6', 'Gsus4', 'G'],
    MAJ2: ['C', 'C/B', 'C/A', 'C/G', 'Fadd9', 'Fmi', 'Csus4', 'Ami7', 'Emi', 'F', 'Gsus4', 'G6'],
    MAJ3: ['C', 'Ami', 'Fma7', 'Gsus4', 'Ami add9', 'F6', 'Csus2', 'G', 'Dsus2', 'Bb add9', 'Gsus4', 'Fadd9'],
    MAJ4: ['C', 'G', 'Ami', 'F6', 'F', 'Ami/E', 'Dmi7', 'Ami/C', 'Gadd9', 'Ami7', 'G/B', 'Dmi/G'],
    MAJ5: ['C', 'D', 'F', 'C', 'Ab', 'Eb', 'Bb', 'F', 'G7sus4', 'Bb add9', 'F6', 'Cadd9'],
    MAJ6: ['C', 'G', 'Dmi', 'Ami', 'F', 'G/F', 'C/E', 'Ami7', 'Dmi7', 'Emi7', 'C/F', 'Gsus4'],
    MAJ7: ['C', 'G', 'Ami', 'Emi', 'F', 'C/E', 'Dmi', 'Dmi/C', 'G7/B', 'G', 'F/A', 'G7/B'],
    MAJ8: ['Cma9', 'C#dim', 'Dmi9', 'D#dim7', 'Emi9', 'C9#5', 'Fma7(add13)', 'Bb9', 'Emi7', 'A9', 'Dmi11', 'G7(b9,b13)'],
    MIN1: ['Cmi', 'Cmi/Eb', 'Fmi', 'G', 'Abma7', 'Eb', 'Gmi', 'Bb', 'F', 'Fmi/Ab', 'Cmi/G', 'G'],
    MIN2: ['Cmi', 'G+/B', 'Cmi/Bb', 'Cmi/A', 'Abma7', 'Ebma7', 'Fmi', 'Bb7', 'Cmi', 'Bbadd9', 'Abadd9', 'G7sus4'],
    MIN3: ['Cmi', 'Ab', 'Eb', 'Bb', 'F', 'Fmi', 'Cmi/G', 'Gsus4', 'Cmi', 'Cmi#5', 'Cmi6', 'Cmi7'],
    MIN4: ['Cmi', 'Eb', 'Bb', 'F', 'Ab', 'Abma7', 'Abmi7', 'Ebma7', 'Dsus4', 'D', 'Fmi/G', 'G+'],
    MIN5: ['Cmi', 'Bb', 'Ab6', 'Bb add9', 'Cmi', 'Dmi7', 'Cmi/Eb', 'Fmi', 'G', 'Ab ma7', 'B6/9', 'Csus4'],
    MIN6: ['Cmi', 'Fmi', 'Bb', 'Eb', 'Ab', 'Dmi7(b5)', 'Gadd(b9)', 'G', 'Ab/G', 'G7', 'Cmi/G', 'G7(b9)'],
    MIN7: ['Cmi9', 'Ab9', 'Cmi11', 'C7(#9,b13)', 'Fmi9', 'Ebma7/F', 'C11', 'Ami11', 'Ab7#11', 'G7#9', 'Cmiadd9', 'G7(b9,b13)'],
    MIN8: ['Cmi6/9', 'Dmi7(b5)', 'Cmi11/G', 'Cmi9', 'Fmi9', 'Abmi7', 'Ebmi7', 'Bbmi7(b5)', 'Ami11', 'Abma7#5', 'G7(b9,b13)', 'Cmi9ma7'],
};

1. Transposable Chord Sets for Major and Minor Keys

Maschine's chord matrix has 192 chords that can be transposed by the root note: sets MAJ1 to MAJ8 for major keys and MIN1 to MIN8 for minor keys. Each set has 12 chords, all originally in the key of C, making it easier to change keys later. I began with simple arrays planning to convert them at a later stage into objects that contain more details like pad number, chord name, roman numeral, and smart key. Moving from arrays to objects ensures future scalability and flexibility in any updated versions of this tool.

function transposeChord(chord, interval) {

    const rootMatch = chord.match(/^[A-G][b#]?/); // Extract the root note (e.g., C, D#, Gb) from the beginning of the chord string
    if (!rootMatch) return chord; // If no root note is found, return the original chord as-is

    const root = rootMatch[0]; // Assign the extracted root note to a variable
    const originalNote = noteMap[root]; // Get the numeric representation of the root note from the noteMap
    const transposedNote = (originalNote + interval + 12) % 12; // Calculate the transposed note value, wrapping around the 12-tone scale
    const transposedRoot = reverseNoteMap[transposedNote]; // Get the note name for the transposed value from reverseNoteMap
    const finalRoot = enharmonicMap[transposedRoot] || transposedRoot; // Map the transposed root to its enharmonic equivalent if available, otherwise keep it as-is

    if (chord.includes('/')) { // Check if the chord contains a slash notation (e.g., /G, /Bb)
        const slashMatch = chord.match(/\/([A-G][b#]?)/); // Extract the note after the slash
    if (slashMatch) { 
        const slashNote = slashMatch[1]; // Assign the extracted slash note to a variable
        const originalSlashNote = noteMap[slashNote]; // Get the numeric representation of the slash note from the noteMap
        const transposedSlashNote = (originalSlashNote + interval + 12) % 12; // Calculate the transposed slash note value, wrapping around the 12-tone scale
        const transposedSlash = reverseNoteMap[transposedSlashNote];  // Get the note name for the transposed slash value from reverseNoteMap
        const finalSlash = enharmonicMap[transposedSlash] || transposedSlash; // Map the transposed slash to its enharmonic equivalent if available, otherwise keep it as-is
        return `${finalRoot}${chord.slice(root.length).split('/')[0]}/${finalSlash}`;  // Return the transposed chord with the transposed slash note
    }
}

    return chord.replace(root, finalRoot); // If there is no slash notation, return the chord with the transposed root note
}

To match Maschine's layout, I needed the tool to automatically adjust all 192 chords based on a given song key while maintaining the the hard coded harmonic structure of every chord bank. This challenge stumped me for some time, but I eventually figured it out. Once I did, other parts of the project came together more easily.

2. Chord Cloning and Simplification

I then developed functions to simplify the transposed chords for use with the Circle of Fifths function I would soon create. This way, with both simplified and more complex versions of the chords for reference makes it easier for the tool to search and provide harmonically sound suggestions. This led me to focus on efficiency to ensure my function only matched chords in their base format - 'Bbmi' as opposed to more complex chords like: 'Bbmi7b5#9'.

function simplifyChord(chord) {
    const rootMatch = chord.match(/^[A-G][b#]?/); // Extract the root note (e.g., C, D#, Gb) from the beginning of the chord string
    if (!rootMatch) return chord; // If no root note is found, return the original chord as-is

    const root = rootMatch[0]; // Assign the extracted root note to a variable
    const isMinor = chord.includes('mi') && !chord.includes('maj'); // Check if the chord is minor (contains 'mi' but not 'maj')

    specificSuffixes.forEach(suffix => { // Iterate over specific suffixes to remove them from the chord
    const regex = new RegExp(suffix + '(?!\w)', 'gi');  // Create a regular expression for the suffix and remove it from the chord
    chord = chord.replace(regex, '');
});

    chord = chord.replace(/\/[A-G][b#]?/g, ''); // Remove any slash chords (e.g., /G, /Bb) from the chord
    const finalRoot = enharmonicMap[root] || root; // Map the root to its enharmonic equivalent if available, otherwise keep the root as-is

    return isMinor ? `${finalRoot}mi${suffixMatch}` : `${finalRoot}${suffixMatch}`.trim();  // Return the simplified chord, appending 'mi' if it is a minor chord
}

This attention to detail allowed me to maintain a balance between providing enough chord info for advanced users while ensuring accessibility for those with less music theory knowledge. By simplifying complex chords and mirroring their base counterparts, users can experiment with different variations without feeling overwhelmed, fostering both creativity and learning.

3. Identifying Relative and Neighboring Chord Matches

Creating a logical Circle of Fifths was perhaps the most crucial part of building this tool. I spent a lot of time cross-referencing, debugging, and refactoring until I resolved issues like mismatched suffixes and incorrect or misordered output. Fixing these problems taught me to take things step-by-step—an approach that was challenging for me but ultimately made for a smoother and more effective process.

// Function to find a chord in the Circle of Fifths
function circleOfFifths(chordSet, currentChord) {

    // Check if a chord is provided, if not log a message and return null
    if (!currentChord) {
        console.log('No chord provided.');
        return null;
    }

    // Define the Circle of Fifths with major, minor, and enharmonic equivalents
    const circle = [
        { major: 'C', minor: 'Am', enharmonicMajor: 'B#', enharmonicMinor: null },
        { major: 'G', minor: 'Em', enharmonicMajor: null, enharmonicMinor: null },
        { major: 'D', minor: 'Bm', enharmonicMajor: null, enharmonicMinor: null },
        { major: 'A', minor: 'F#m', enharmonicMajor: null, enharmonicMinor: 'G#m' },
        { major: 'E', minor: 'C#m', enharmonicMajor: null, enharmonicMinor: 'Dbm' },
        { major: 'B', minor: 'G#m', enharmonicMajor: 'Cb', enharmonicMinor: 'Abm' },
        { major: 'F#', minor: 'D#m', enharmonicMajor: 'Gb', enharmonicMinor: 'Ebm' },
        { major: 'Db', minor: 'Bbm', enharmonicMajor: 'C#', enharmonicMinor: 'A#m' },
        { major: 'Ab', minor: 'Fm', enharmonicMajor: 'G#', enharmonicMinor: null },
        { major: 'Eb', minor: 'Cm', enharmonicMajor: 'D#', enharmonicMinor: null },
        { major: 'Bb', minor: 'Gm', enharmonicMajor: 'A#', enharmonicMinor: null },
        { major: 'F', minor: 'Dm', enharmonicMajor: 'E#', enharmonicMinor: null }
    ];

    // Extract the root note of the current chord (e.g., 'C' from 'Cmaj7')
    const simplifiedRoot = currentChord.match(/^[A-Ga-g][b#]?/)[0];
    let currentKey = null;
    let chordType = '';

    // Loop through the Circle of Fifths to find a matching key
    for (let i = 0; i < circle.length; i++) {
        // Check if the chord is a major or its enharmonic equivalent
        if (circle[i].major === simplifiedRoot || circle[i].enharmonicMajor === simplifiedRoot) {
            currentKey = circle[i];
            chordType = 'major';
            break;
        // Check if the chord is a minor or its enharmonic equivalent
        } else if (circle[i].minor === simplifiedRoot || circle[i].enharmonicMinor === simplifiedRoot) {
            currentKey = circle[i];
            chordType = 'minor';
            break;
        }
    }

    // If no matching key is found, log a message and return null
    if (!currentKey) {
        console.log('Chord not found in the circle of fifths.');
        return null;
    }
}

Reverse engineering these chord banks allowed me to create a more intuitive way of accessing the Circle of Fifths without needing to know how to read it!

With 'Fif' Chord Finder' users can easily find harmonically related chords and explore progression options, guaranteeing smoother transitions and richer musical compositions.

So...What’s Next?

Although I’ve made significant progress, there's still more work ahead. Moving forward, I plan to create a mobile-responsive React app, with many more features beyond the basic 'Chord Finder' feature. For example, I'm considering including pad thumbnails that appear on hover and design a visual interface that mirrors Maschine hardware, making the experience as user-friendly as possible.

My ultimate goal is to bridge the gap between an artists musical ideas and what they record, not only making music theory more accessible, but empowering creativity for anyone else like me!

Here are some tags for this post:

Back to Home

Man V Maschine_Ch 1

app updates. reflections. creative.